Trong toán học và tin học, đồ thị là đối tượng nghiên cứu cơ bản của lý thuyết đồ thị. Một cách không chính thức, đồ thị là một tập các đối tượng gọi là đỉnh nối với nhau bởi các cạnh. Thông thường, đồ thị được vẽ dưới dạng một tập các điểm (đỉnh, nút) nối với nhau bởi các đoạn thẳng (cạnh). Tùy theo ứng dụng mà một số cạnh có thể có hướng.
Sơ lược các khái niệm cơ bản về đồ thị
Một cách không chính thức, đồ thị là một tập các đối tượng được gọi là các đỉnh nối với nhau bởi các cạnh.
Một đồ thị kí hiệu là
\[G=(V, E)\]Trong đó:
-
\( V \) là tập các đỉnh của đồ thị. Đặt \( \mid V \mid = n \) (số đỉnh).
-
\( E \) là tập các cạnh của đồ thị. Đặt \( \mid E \mid = m \) (số cạnh).
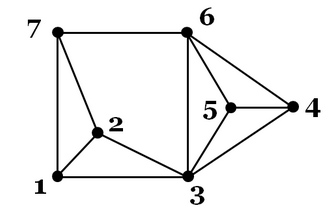
Đỉnh:
Đỉnh biểu diễn các đối tượng trong đồ thị, thường được đánh dấu bằng các số hoặc kí hiệu bằng các chữ cái in thường u,v,…
Cạnh:
Cạnh nối đỉnh x với đỉnh y là một tập gồm hai phần tử \( {x, y} \), thường được vẽ dưới dạng một đoạn thẳng nối hai đỉnh.
Cạnh có hướng (cung):
Là một cặp đỉnh có thứ tự. Trong mỗi cặp có thứ tự đó, đỉnh thứ nhất được gọi là đỉnh đầu, đỉnh thứ hai là đỉnh cuối.
Cạnh vô hướng:
Không quan tâm đến hướng và coi hai đỉnh như nhau.
Khuyên:
Là một cạnh nối một đỉnh với chính nó.
Hai cạnh song song:
Là hai cạnh cùng nối hai đỉnh u, v.
Đồ thị có hướng:
Là đồ thị mà tất cả các cạnh trong đồ thị đều có hướng.
Đồ thị vô hướng:
Là đồ thị mà tất cả các cạnh trong đồ thị đều vô hướng.
Đơn đồ thị:
Là đồ thị không có khuyên và không có cạnh song song.
Đa đồ thị:
Là đồ thị không phải là đơn đồ thị.
Bậc:
Trong đồ thị vô hướng, bậc của đỉnh v trong đồ thị G, ký hiệu \( d_G(u) \), là số cạnh liên thuộc với v, trong đó, khuyên được tính hai lần.
Ta có định lí:
Giả sử \( G=(V, E) \) là đồ thị vô hướng, khi đó tổng các bậc đỉnh trong V sẽ bằng 2 lần số cạnh.
\[\sum_{ v \in V }{ d_G(v) } = m * 2\]Hệ quả: Trong đồ thị vô hướng, số đỉnh bậc lẻ là chẵn.
Trong đồ thị có hướng, ta định nghĩa bán bậc ra của u là số cung đi ra khỏi nó, kí hiệu \( d^+_G(u) \), bán bậc vào của u là số cung đi ra khỏi nó, kí hiệu \( d^-_G(u) \).
Giả sử \( G=(V, E) \) là đồ thị có hướng, khi đó tổng các bán bậc vào bằng tổng các bán bậc ra và bằng số cung của đồ thị.
\[\sum_{ v \in V }{ d^+_G(v) } = \sum_{ v \in V }{ d^+_G(v) } = m\]Đường đi và chu trình:
Một dãy các đỉnh P = (p0,p1,…,pk) sao cho (Pi-1, Pi) ∊ E, ∀i: 1<=i<=k được gọi là một đường đi.
Một đường đi là chu trình khi p0 = pk.
Liên thông:
Một đồ thị vô hướng là liên thông nếu tồn tại đường đi giữa hai cặp đỉnh bất kì thuộc đồ thị.
Một đồ thị có hướng là liên thông nếu phiên bản vô hướng của đồ thị đó là liên thông.
Đồ thị phẳng:
Đồ thị phẳng là đồ thị có thể được vẽ trên mặt phẳng sao cho không có hai đỉnh nào trùng nhau và các cạnh nào trùng nhau hoặc cắt nhau.
Công thức Euler:
Giả sử đồ thị vô hướng liên thông \( G=(V, E) \) là đồ thị phẳng, với n đỉnh và m cạnh chia mặt phẳng thành e phần thì
\[n - m + e = 2\]Biểu diễn đồ thị trên máy tính:
Có nhiều cách để biểu diễn đồ thị trên máy tính, tùy thuộc vào tính chất của đồ thị hoặc thuật toán áp dụng với đồ thị… Ta cũng có thể lưu kèm theo các thông tin như trọng số, giá trị phù hợp với từng cạnh. Dưới đây là một vài cách phổ biến.
Ma trận kề:
Tạo một ma trận A kích thước n*n trong đó n là số đỉnh của đồ thị. Ta gán a[u][v] = 0 nếu có cạnh cạnh nối hai đỉnh u, v.
Nếu đồ thị là đa đồ thị, ta có thể gán a[u][v] = số cạnh nối u và v.
Định nghĩa và gán tùy theo lập trình viên hiểu là vô hướng hay có hướng, đơn đồ thị hay đa đồ thị.
- Ưu điểm:
- Để kiểm tra hai đỉnh u, v có kề nhau không, ta chỉ cần kiểm tra trong độ phức tạp \( O(1) \).
- Nhược điểm:
- Dù đồ thị có nhiều cạnh hay ít cạnh thì cũng phải mất n*n ô nhớ để lưu.
- Để duyệt tất cả các đỉnh kề với u, ta phải duyệt tất cả các đỉnh v ∊ V cho dù đỉnh u kề với ít hoặc không kề với đỉnh nào khác.
Biểu diễn bằng ma trận kề thường được dùng khi đồ thị có ít đỉnh, hoặc đồ thị dày, nhiều cạnh, hoặc thuật toán để thao tác trên đồ thị yêu cầu.
Danh sách cạnh:
Với đồ thị \( G=(V, E) \) có n đỉnh, m cạnh, ta có thể liệt kê tất cả các cạnh của đồ thị bằng một danh sách tương ứng, mỗi phần tử của mảng tương ứng là một cặp (u,v) là một cạnh thuộc E, tùy theo người lập trình định nghĩa là có hướng hay vô hướng.
- Ưu điểm:
- Với đồ thị thưa, ta chỉ cần mất m (số lượng cạnh) ô nhớ để lưu đồ thị.
- Nhược điểm:
- Khi cần kiểm tra hai đỉnh u,v có kề nhau hay không, ta không thể kiểm tra nhanh trong //( O(1) //) như cách lưu bằng ma trận kề, mặc dù tùy theo cách lưu danh sách cạnh mà ta có thể kiểm tra trong //( O(logn) //) hoặc ít hơn.
Danh sách kề:
Với mỗi đỉnh của đồ thị, ta lưu một danh sách các đỉnh kề với đỉnh đó.
- Ưu điểm:
- Với phương pháp này, việc duyệt tất cả các đỉnh kề với đỉnh u vô cùng dễ dàng.
- Nhược điểm:
- Khi cần kiểm tra hai đỉnh u,v có kề nhau hay không, ta không thể kiểm tra nhanh trong \( O(1) \) như cách lưu bằng ma trận kề, mặc dù tùy theo cách lưu danh sách cạnh mà ta có thể kiểm tra trong \( O(logn) \) hoặc ít hơn.
Phần sau: [Lý thuyết đồ thị cơ bản] Phần 2: Tìm kiếm theo chiều rộng trên đồ thị - Breadth-First Search (BFS)